What is Insertion Sort?

Insertion sort is a straightforward sorting algorithm that constructs the final sorted array one item at a time. It operates by splitting the input array into two parts: sorted and unsorted. The method then continually inserts the first unsorted element into the right location in the sorted section, moving the remaining elements to make room.

Algorithm:

The algorithm works as follows:

1. Let arr be the input array of length n
2. For i = 1 to n-1:
   • a. Set key to the i-th element of arr
   • b. Set j to i-1
   • c. While j >= 0 and arr[j] > key: i. Set arr[j+1] to arr[j] ii. Decrement j by 1
   • d. Set arr[j+1] to key
3. The sorted array is now arr

The inner loop (step 2c) shifts the elements to the right to create the correct position for the current element. The outer loop (step 2) selects each element in turn and ensures that it is in the correct position.

Time Complexity:

• Worst case: O(n^2)
• Best case: Ω(n)
• Average case: Θ(n^2)

Implementation of the algorithm in Java:

public static void insertionSort(int[] arr) {
    int n = arr.length;
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;
    }
}

Problems based on Insertion Sort:

• Given the head of a singly linked list, sort the list using insertion sort, and return the sorted list’s head.

Example:

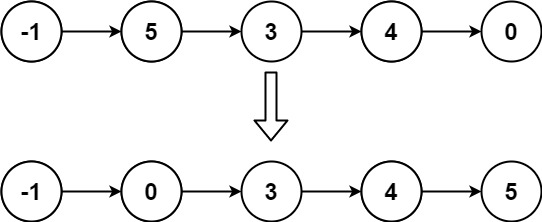
Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]

Solution:

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
   public ListNode insertionSortList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }

    ListNode dummy = new ListNode(0);
    dummy.next = head;

    ListNode sortedTail = head, curr = head.next;
    while (curr != null) {
        if (sortedTail.val <= curr.val) {
            sortedTail = sortedTail.next;
        } else {
            ListNode prev = dummy;
            while (prev.next.val <= curr.val) {
                prev = prev.next;
            }

            sortedTail.next = curr.next;
            curr.next = prev.next;
            prev.next = curr;
        }
        curr = sortedTail.next;
    }

    return dummy.next;
}

}

In the above implementation,

• we maintain two pointers – sortedTail and curr. sortedTail points to the last node in the sorted section, and curr points to the first node in the unsorted section.
• compare the value of sortedTail with curr. If sortedTail.val is less than or equal to curr.val, then curr is already in the correct position, and we move both sortedTail and curr to their next nodes.

• Given a shuffled sentence s containing no more than 9 words, reconstruct, and return the original sentence.

For example, the sentence "This is a sentence" can be shuffled as "sentence4 a3 is2 This1" or "is2 sentence4 This1 a3".

Solution:

class Solution {
    public String sortSentence(String s) {
        String[] words = s.split(" ");
    int n = words.length;
    for (int i = 1; i < n; i++) {
        String current = words[i];
        int j = i - 1;
        while (j >= 0 && getIndex(words[j]) > getIndex(current)) {
            words[j+1] = words[j];
            j--;
        }
        words[j+1] = current;
    }
    StringBuilder sb = new StringBuilder();
    for (String word : words) {
        sb.append(word.substring(0, word.length()-1)).append(" ");
    }
    sb.setLength(sb.length()-1); // remove the extra space at the end
    return sb.toString();
}

private static int getIndex(String word) {
    int len = word.length();
    return Integer.parseInt(word.substring(len-1));
    }
}

• We began by dividing the shuffled phrase s into an array of words by using the space character as a delimiter.
• Then, using insertion sort, we run through the array and sort the words depending on their index, which we obtained using the getIndex helper method.
• Finally, we rebuild the original phrase by concatenating the sorted words without their indexes and returning the final string.

Note: also read about Selection Sort

Follow Me

Please follow me to read my latest post on programming and technology if you like my post.

https://www.instagram.com/coderz.py/

https://www.facebook.com/coderz.py