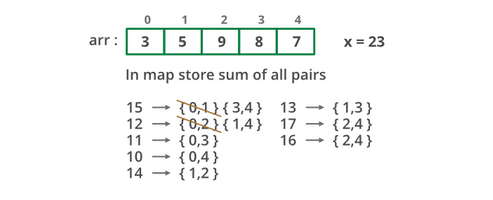
Problem
Given an integer array, output all the unique pairs that sum up to a specific value k.
So the input:
pair_sum([1,3,2,2],4)
would return 2 pairs:
(1,3)
(2,2)
Solution
The O(N) algorithm uses the set data structure. We perform a linear pass from the beginning and for each element we check whether k-element is in the set of seen numbers. If it is, then we found a pair of sum k and add it to the output. If not, this element doesn’t belong to a pair yet, and we add it to the set of seen elements.
The algorithm is really simple once we figure out using a set. The complexity is O(N) because we do a single linear scan of the array, and for each element we just check whether the corresponding number to form a pair is in the set or add the current element to the set. Insert and find operations of a set are both average O(1), so the algorithm is O(N) in total.
def pair_sum(arr,k):
if len(arr)<2:
return
# Sets for tracking
seen = set()
output = set()
# For every number in array
for num in arr:
# Set target difference
target = k-num
# Add it to set if target hasn't been seen
if target not in seen:
seen.add(num)
else:
# Add a tuple with the corresponding pair
output.add( (min(num,target), max(num,target)) )
# FOR TESTING
return len(output)
# Nice one-liner for printing output
#return '\n'.join(map(str,list(output)))
pair_sum([1,3,2,2],4)
2
Test Your Solution
"""
RUN THIS CELL TO TEST YOUR SOLUTION
"""
from nose.tools import assert_equal
class TestPair(object):
def test(self,sol):
assert_equal(sol([1,9,2,8,3,7,4,6,5,5,13,14,11,13,-1],10),6)
assert_equal(sol([1,2,3,1],3),1)
assert_equal(sol([1,3,2,2],4),2)
print('ALL TEST CASES PASSED')
#Run tests
t = TestPair()
t.test(pair_sum)
ALL TEST CASES PASSED
Recommended: Understand Big-O Notation Complexity Of Algorithm
Follow Me ❤😊
If you like my post please follow me to read my latest post on programming and technology.
Leave a Comment
You must be logged in to post a comment.