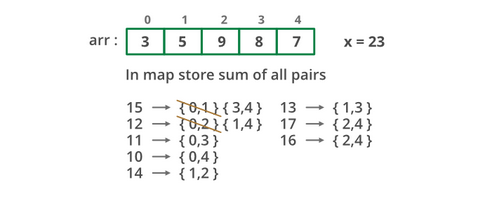
Problem

Given an integer array, output all the unique pairs that sum up to a specific value k.

So the input:

pair_sum([1,3,2,2],4)

would return 2 pairs:

(1,3)
(2,2)

Solution

The O(N) algorithm uses the set data structure. We perform a linear pass from the beginning and for each element we check whether k-element is in the set of seen numbers. If it is, then we found a pair of sum k and add it to the output. If not, this element doesn’t belong to a pair yet, and we add it to the set of seen elements.

The algorithm is really simple once we figure out using a set. The complexity is O(N) because we do a single linear scan of the array, and for each element we just check whether the corresponding number to form a pair is in the set or add the current element to the set. Insert and find operations of a set are both average O(1), so the algorithm is O(N) in total.

def pair_sum(arr,k):
    
    if len(arr)<2:
        return
    
    # Sets for tracking
    seen = set()
    output = set()
    
    # For every number in array
    for num in arr:
        
        # Set target difference
        target = k-num
        
        # Add it to set if target hasn't been seen
        if target not in seen:
            seen.add(num)
        
        else:
            # Add a tuple with the corresponding pair
            output.add( (min(num,target),  max(num,target)) )
    
    
    # FOR TESTING
    return len(output)
    # Nice one-liner for printing output
    #return '\n'.join(map(str,list(output)))

pair_sum([1,3,2,2],4)

2

Test Your Solution

"""
RUN THIS CELL TO TEST YOUR SOLUTION
"""
from nose.tools import assert_equal

class TestPair(object):
    
    def test(self,sol):
        assert_equal(sol([1,9,2,8,3,7,4,6,5,5,13,14,11,13,-1],10),6)
        assert_equal(sol([1,2,3,1],3),1)
        assert_equal(sol([1,3,2,2],4),2)
        print('ALL TEST CASES PASSED')
        
#Run tests
t = TestPair()
t.test(pair_sum)

ALL TEST CASES PASSED

Recommended: Understand Big-O Notation Complexity Of Algorithm

Follow Me ❤😊

If you like my post please follow me to read my latest post on programming and technology.

Instagram

Facebook

Hassan Raza