What is a 2D Array?

• A 2D matrix is a two-dimensional array that contains rows and columns in data structures and methods. It is also known as a two-dimensional array.
• A matrix can be represented in code as a 2D array, where each element of the array is itself an array, and each row of the matrix is represented by an inner array.
• Column major matrix is a two-dimensional array in which entries are stored column by column.
• Row major matrix is a two-dimensional array in which elements are stored row by row.

Let’s understand it better through the given diagram:

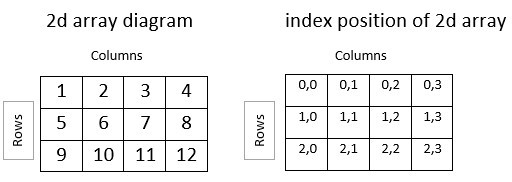
Note: Working with 2D matrices frequently involves iterating over the matrix’s rows and columns and executing operations on the individual elements.

Need of 2D Arrays in DSA:

Here are some of the reasons why 2D arrays are important in data structures and algorithms:

• Storing and accessing data
• Image processing where images are represented as matrices of pixel values.
• Graphs can be represented using 2D arrays where the rows and columns represent the vertices, and the elements represent the edges connecting the vertices.
• Two-dimensional arrays are used in dynamic programming where the problem is solved by breaking it down into smaller subproblems that are solved and stored in a 2D table.
• Matrices can be represented as 2D arrays in algorithms such as matrix multiplication, Gaussian elimination, and matrix inversion.

Let us now discuss various 2D matrix examples:

Program to return all elements of the matrix in spiral order:

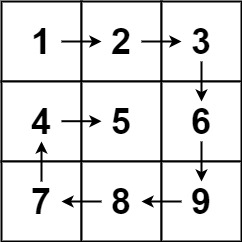
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Solution:

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) 
{
     int n = matrix.length;
    int m = matrix[0].length;
    ArrayList<Integer> arr = new ArrayList<>();
    int top = 0 ;
    int bottom = n-1;
    int right = m-1;
    int left = 0;
    while(top<=bottom && left<=right){
       for(int i = left ; i<=right ;i++){
            arr.add(matrix[top][i]);    
         }
        top++;
        for(int i  = top ;i<=bottom;i++ ){
            arr.add(matrix[i][right]);
        }
        right--;
        if(top<=bottom){
            for(int i = right;i>=left;i--){
                arr.add(matrix[bottom][i]);
            }
            bottom--;
        }
      if(left<=right){

            for(int i = bottom;i>=top;i--){
                arr.add(matrix[i][left]);
            }
            left++;
        }
    }
    return arr;
}
     public static void main(String[] args) {
     Solution obj= new Solution();
     Scanner sc= new Scanner (System.in);
     int array[][] = new int[3][3];   
    // Read the matrix values   
    System.out.println("Enter the elements of the array: ");   
      //loop for row  
    for (int i = 0; i < 3; i++)   {
      //inner for loop for column  
      for (int j = 0; j < 3; j++)   
        array[i][j] = sc.nextInt(); 
      }     
      System.out.println(obj.spiralOrder(array));
    }
 }

To print the matrix in spiral the loop iterates through the matrix in four directions:

1. Traverse from left to right: This loop iterates from left to right, adding each element to the arr ArrayList.
2. Traverse from top to bottom: This loop iterates from top to bottom, adding each element to the arr ArrayList.
3. Traverse from right to left: This loop iterates from right to left, adding each element to the arr ArrayList.
4. Traverse from bottom to top: This loop iterates from bottom to top, adding each element to the arr ArrayList.

Program to rotate the image by 90 degrees (clockwise):

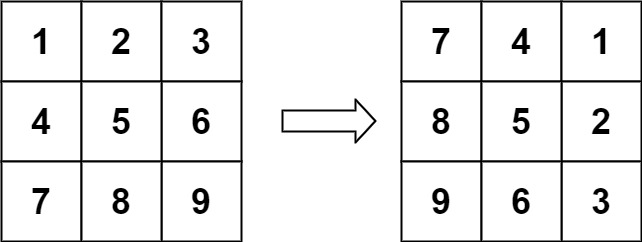
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Solution:

public class Solution {
    public void rotate(int[][] M) {
        for (int i = 0; i < (M.length+1)/2; i++) {
            for (int j = 0; j < M.length/2; j++) {
                int tmp = M[i][j];
                M[i][j] = M[M.length-j-1][i];
                M[M.length-j-1][i] = M[M.length-i-1][M.length-j-1];
                M[M.length-i-1][M.length-j-1] = M[j][M.length-i-1];
                M[j][M.length-i-1] = tmp;
            }
        }
    }
}

Instead of using the longer method, the approach used in this solution is to divide the matrix into smaller concentric squares and rotate each square individually. That is,

• The outermost square is rotated first, followed by the next inner square, and so on.
• For each square, we use four temporary variables to store the values of the four corners, and then perform a cyclic rotation of the values in that square.

Note: also read about DSA: SubArray

Follow Me

Please follow me to read my latest post on programming and technology if you like my post.

https://www.instagram.com/coderz.py/

https://www.facebook.com/coderz.py