What is Tree Data Structure?

• A tree data structure is made up of nodes that are connected via edges.
• The root node is the topmost node in a tree, and it is connected to zero or more child nodes.
• Each child node can have zero or more child nodes attached to it, establishing a hierarchical structure.
• Leaf nodes are nodes that have no child nodes.
• Except for the root node, which has no parent node, each node in a tree can have only one parent node.
• Siblings are nodes that share the same parent node.
• The number of edges from the root node to a node is its depth, and the height of a tree is the maximum depth of any node in the tree.

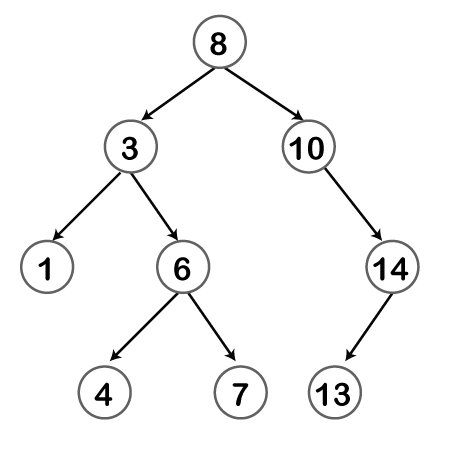
Basic terms used in Tree data structure:

Some basic terms used in tree data structure are:

1. Node: Each element in a tree is called a node.
2. Node degree: The number of direct children of a node is called the degree of that node. For example, in the above tree, the degree of node 2 is 2 because it has two children.
3. Root: The root node is the topmost node in the tree hierarchy. In other words, the root node is the one that doesn’t have any parent.
4. Parent: The node which is one level above any node is called its parent i.e. If the node contains any sub-node, then that node is said to be the parent of that sub-node.
5. Child: If the node is a descendant of any node, then the node is known as a child node.
6. Siblings: Nodes that share the same parent are called siblings.
7. Leaf: A node that does not have any children is called a leaf node or a terminal node.
8. Subtree: A tree consisting of a node and all its descendants is called a subtree.
9. Depth: The number of edges from the root to a given node is called its depth.
10. Height: The number of edges on the longest path from a node to a leaf is called its height.
11. Ancestor: A node that is on the path from the root to a given node is called an ancestor of that node.
12. Descendant: A node that is below a given node in a tree is called a descendant of that node.

Implementation of Tree:

There are two main ways to implement trees: using an array and using linked lists.

• Array Implementation: A binary tree is represented by an array in the array implementation. The root node is saved at index 1, the left child of a node at index i is stored at index 2i, and the right child of a node at index i is stored at index 2i+1. This technique is typically used for complete binary trees, where all levels but the last are filled.

class BinaryTree {
    int[] tree;
    int size;

    public BinaryTree(int size) {
        this.size = size;
        this.tree = new int[size + 1]; // add 1 for 1-indexing
    }

    // insert a new node into the tree
    public void insert(int value) {
        if (size == tree.length - 1) {
            System.out.println("Tree is full.");
            return;
        }
        size++;
        tree[size] = value;
    }

    // get the value of the parent node of a given index
    public int parent(int index) {
        return tree[index / 2];
    }

    // get the value of the left child node of a given index
    public int leftChild(int index) {
        return tree[2 * index];
    }

    // get the value of the right child node of a given index
    public int rightChild(int index) {
        return tree[2 * index + 1];
    }
}

Time Complexity:O(1)
Space Complexity: O(n)

• Linked List Implementation: Each node of the tree is represented as a separate object or node in the linked list implementation, having references or pointers to its sibling nodes. There are two kinds of linked list implementations:

• Singly Linked List: Each node has a reference to only one child node, i.e., either the left child or the right child.
• Doubly Linked List: Each node has references to both the left and the right child nodes.

public class TreeNode {
    int data;
    TreeNode leftChild;
    TreeNode rightChild;

    public TreeNode(int data) {
        this.data = data;
        this.leftChild = null;
        this.rightChild = null;
    }
}

public class BinaryTree {
    TreeNode root;

    public BinaryTree() {
        root = null;
    }

    public void insert(int data) {
        TreeNode newNode = new TreeNode(data);

        if (root == null) {
            root = newNode;
        } else {
            TreeNode current = root;
            TreeNode parent;

            while (true) {
                parent = current;

                if (data < current.data) {
                    current = current.leftChild;

                    if (current == null) {
                        parent.leftChild = newNode;
                        return;
                    }
                } else {
                    current = current.rightChild;

                    if (current == null) {
                        parent.rightChild = newNode;
                        return;
                    }
                }
            }
        }
    }

    public void printInorderTraversal(TreeNode node) {
        if (node != null) {
            printInorderTraversal(node.leftChild);
            System.out.print(node.data + " ");
            printInorderTraversal(node.rightChild);
        }
    }

    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();

        binaryTree.insert(50);
        binaryTree.insert(30);
        binaryTree.insert(70);
        binaryTree.insert(20);
        binaryTree.insert(40);
        binaryTree.insert(60);
        binaryTree.insert(80);

        System.out.print("Inorder Traversal: ");
        binaryTree.printInorderTraversal(binaryTree.root);
    }
}

Time Complexity: O(log n) to O(n) for insertion and O(n) for inorder traversal

Space Complexity: O(n)

Tree traversal techniques:

In tree data structure, there are two main traversal techniques:

1. Depth-First Traversal: We study the deepest nodes of the tree data structure first, then progress up towards the root node in depth-first traversal. This technique is mostly used to investigate the structure of a tree.

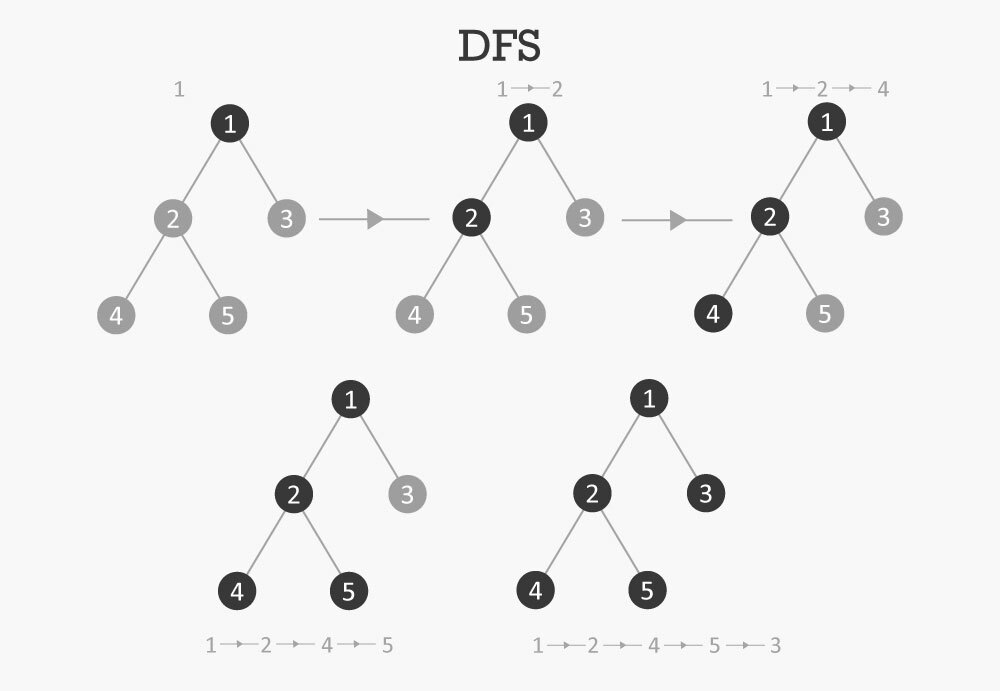
There are three types of depth-first traversal:

• Inorder Traversal: In inorder traversal, we first traverse the left subtree, then the root node and then the right subtree.

 public void inorderTraversal(Node node) {
        if (node == null) {
            return;
        }
        inorderTraversal(node.left);
        System.out.print(node.data + " ");
        inorderTraversal(node.right);
    }

• Preorder Traversal: In preorder traversal, we first traverse the root node, then the left subtree and then the right subtree.

  public void printPreorder(Node node) {
        if (node == null)
            return;
        
        System.out.print(node.data + " ");
        printPreorder(node.left);
        printPreorder(node.right);
    }

• Postorder Traversal: In postorder traversal, we first traverse the left subtree, then the right subtree and then the root node.

void postorder(Node node) {
        if (node == null)
            return;
 
        // Traverse left subtree
        postorder(node.left);
 
        // Traverse right subtree
        postorder(node.right);
 
        // Visit root node
        System.out.print(node.data + " ");
    }

2. Breadth-First Traversal: In breadth-first traversal, we explore the level of the node by level starting from the root node. This technique is mostly used to locate a node or to determine the shortest path between two nodes.

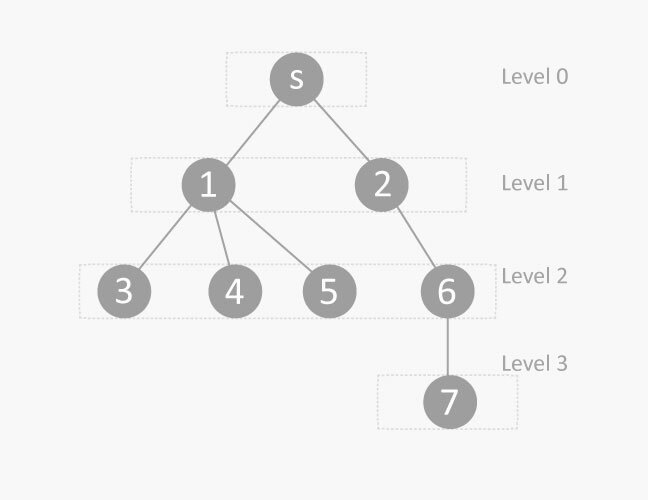
import java.util.LinkedList;
import java.util.Queue;

class Node {
    int value;
    Node left, right;
    
    Node(int value) {
        this.value = value;
        this.left = this.right = null;
    }
}

public class BFS {
    Node root;
    
    BFS() {
        root = null;
    }
    
    void printLevelOrder() {
        if (root == null)
            return;
        
        Queue<Node> queue = new LinkedList<Node>();
        queue.add(root);
        
        while (!queue.isEmpty()) {
            Node node = queue.poll();
            System.out.print(node.value + " ");
            
            if (node.left != null)
                queue.add(node.left);
            
            if (node.right != null)
                queue.add(node.right);
        }
    }
    
    public static void main(String[] args) {
        BFS tree = new BFS();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        
        System.out.println("BFS Traversal of Binary Tree:");
        tree.printLevelOrder();
    }
}

Time Complexity: O(n)

Space Complexity: O(n)

Note: also read about Problems based on Linked List

Follow Me

If you like my post please follow me to read my latest post on programming and technology.

https://www.instagram.com/coderz.py/

https://www.facebook.com/coderz.py