
Problem Statement:
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
Example 1: Input: n = 3 Output: [“((()))”,”(()())”,”(())()”,”()(())”,”()()()”]
Example 2: Input: n = 1 Output: [“()”]
Solution:
This problem can be solved using the concept of backtracking, Let’s see how to approach it.
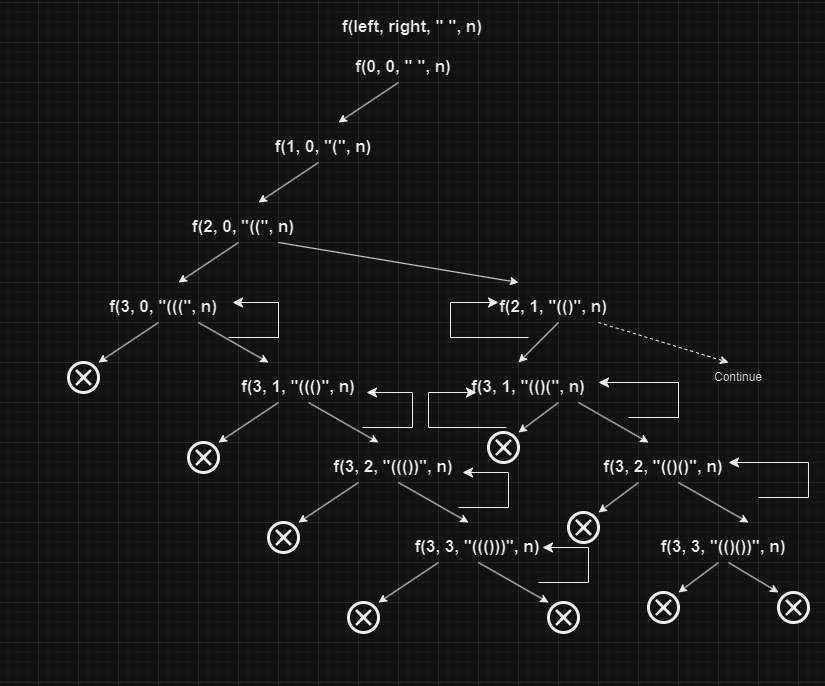
We have to write a function generate([], left, right, str=””, n)
[] -> Stores the result
left -> represents the opening bracket
right -> represents the closing bracket
str -> Stores each bracket in each iteration
n -> Input size
Step 1: Base condition of the recursion if(str. length() == 2*n) add balanced parenthesis string in result = [] and return.
Taking 2*n because for n = 1, str = “()” of size 2, n = 2, str = “(())” of size 4.
Step 2:
check condition (left < n) if it’s true then call function generate([], left + 1, right, str+”(“, n)
Step 3:
check condition (right < left) if it’s true then call function generate([], left, right + 1, str+”)”, n)
Step 4:
In the end, it will give the final result, which contains all combinations of balanced parenthesis.
All the above steps (1, 2, and 3) will repeat until they create all balanced parenthesis combinations.
Note: Try yourself, then look into the code.
class Solution {
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<String>();
dfs(res, 0, 0, "", n);
return res;
}
public void dfs(List<String> res, int left, int right, String s, int n) {
if(s.length() == n*2) {
res.add(s);
return;
}
if(left < n) {
dfs(res, left + 1, right, s + "(", n);
}
if(right < left) {
dfs(res, left, right+1, s + ")", n);
}
}
}
Time Complexity: O(2^n) because of the recursive tree.
Space Complexity: O(1) because there is no extra space taking, only one List<String> which is required as output.
I hope you understand the approach to solving this problem.
Peace ✌️
Leave a Comment
You must be logged in to post a comment.