
What are pointers?
- Pointers are variables that are used to save the position of a value in memory. A memory address is stored in a pointer to a location.
- Pointers are a key notion in data structures and algorithms (DSA) that provide significant memory management and data manipulation capabilities.
- Understanding pointers allows programmers to optimize their algorithms and develop dynamic data structures, opening up new avenues for addressing challenging issues.
Note: Dereferencing is the process of getting the value stored at a location referenced by a pointer.
Need for Pointers in DSA:
Pointers are essential in data structures for several reasons:
- Efficient Memory Management: Pointers enable dynamic memory allocation, which is essential for designing data structures that may expand and contract dynamically during runtime.
- Dynamic Data Structures: Pointers are used to create dynamic data structures such as linked lists, trees, graphs, and hash tables, which makes it easier to link and relate items, allowing for faster traversal, insertion, deletion, and modification actions.
- Indirect Data Access: Pointers offer indirect data access by storing a variable’s memory address. When working with huge data structures, this indirect access is very advantageous since it eliminates the need for copying or transmitting large quantities of data, resulting in enhanced speed and decreased memory cost.
- Sharing and Reusing Data: Multiple data structures or functions can refer to and share the same data using pointers.
- Pointer Arithmetic: Arithmetic operations such as addition, subtraction, and comparison are supported by pointers. These operations make it possible to navigate and manipulate data structures such as arrays, linked lists, and trees efficiently.
- Pass-by-Reference: Pointers enable pass-by-reference in function calls, allowing modifications made to data within a function to be visible outside its scope. This avoids unnecessary data copying, especially when dealing with large objects or complex data structures, leading to improved performance and reduced memory usage.
Types of Pointers:
- NULL Pointer: A NULL pointer is a pointer that does not point to any valid object or memory location. It is often used to represent the absence or invalidity of a pointer. It is commonly used to terminate linked lists or indicate the absence of data.
- VOID Pointer: A void pointer is a generic pointer that can point to objects of any data type. However, it cannot be directly dereferenced since its type is unknown. It is commonly used when a pointer needs to handle different data types, such as in functions that operate on different types of objects.
- WILD Pointer: A wild pointer is a pointer that has not been initialized or points to an arbitrary memory location. It does not refer to a valid object or memory and can lead to unexpected behavior or program crashes. Wild pointers should be avoided as they can introduce bugs and security vulnerabilities.
- Dangling Pointer: A dangling pointer is a pointer that points to a memory location that has been deallocated or is no longer valid. This can occur when the memory block that the pointer refers to has been freed, but the pointer is still being used. Accessing or dereferencing a dangling pointer can lead to undefined behavior.
- Function Pointer: A function pointer is a type of pointer that holds the address of a function rather than a data variable. It allows for dynamic dispatch and enables the calling of different functions at runtime. Function pointers are often used in advanced programming techniques, such as callback functions and implementing polymorphism.
Examples:
Here are a few code examples and implementations to illustrate the practical use of pointers in data structures and algorithms:
- Dynamic Memory Allocation using Pointers:
// Dynamic allocation of an integer array
int size = 5;
int* dynamicArray = (int*)malloc(size * sizeof(int));
// Dynamic allocation of a structure
struct Node {
int data;
struct Node* next;
};
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));- Linked List Implementation using Pointers:
// Node structure for a linked list
struct Node {
int data;
struct Node* next;
};
// Inserting a node at the beginning of the linked list
void insertNode(struct Node** head, int data) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = data;
newNode->next = *head;
*head = newNode;
}- Pointer Arithmetic for Efficient Data Access:
// Accessing elements in an array using pointer arithmetic
int array[] = {1, 2, 3, 4, 5};
int* ptr = array;
// Print array elements using pointer arithmetic
for (int i = 0; i < 5; i++) {
printf("%d ", *(ptr + i));
}- Pass-by-Reference in Function Calls:
// Swapping two integers using pointers
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
int main() {
int x = 5, y = 10;
printf("Before swap: x = %d, y = %d\n", x, y);
swap(&x, &y);
printf("After swap: x = %d, y = %d\n", x, y);
return 0;
}Problems based on Pointers:
Given a binary tree
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example :
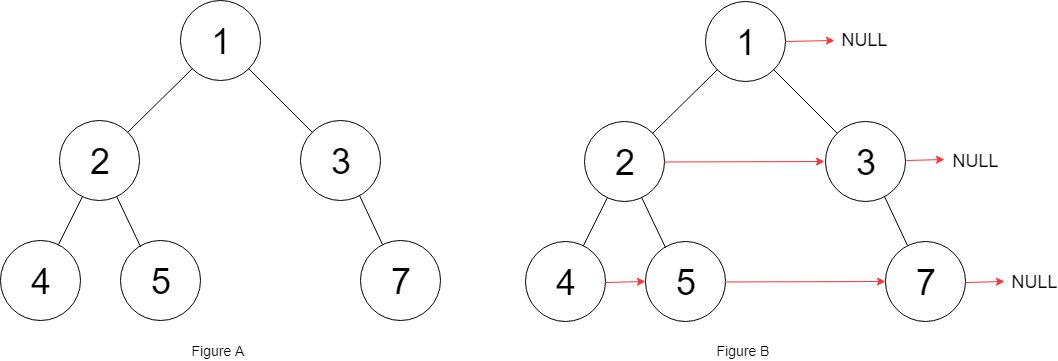
Input: root = [1,2,3,4,5,null,7] Output: [1,#,2,3,#,4,5,7,#] Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
Solution:
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr) {
return nullptr;
}
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int levelSize = q.size();
for (int i = 0; i < levelSize; i++) {
Node* curr = q.front();
q.pop();
if (i < levelSize - 1) {
curr->next = q.front();
}
if (curr->left != nullptr) {
q.push(curr->left);
}
if (curr->right != nullptr) {
q.push(curr->right);
}
}
}
return root;
}
};- This code uses a queue to perform a level-order traversal of the binary tree.
- It connects each node’s
nextpointer to its right node at the same level. - The time complexity of the code is O(N), where N is the number of nodes in the tree, as we visit each node once.
- The space complexity is O(M), where M is the maximum number of nodes at any level in the tree (the maximum size of the queue during the traversal).
Given the head of a linked list, remove the nth node from the end of the list and return its head.
Example:
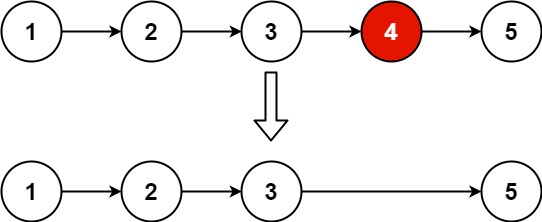
Input: head = [1,2,3,4,5], n = 2 Output: [1,2,3,5]
Solution:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummy = new ListNode(0);
dummy->next = head;
ListNode* fast = dummy;
ListNode* slow = dummy;
// Move fast pointer n nodes ahead
for (int i = 0; i <= n; i++) {
fast = fast->next;
}
// Handle case when n is equal to the length of the list
if (fast == nullptr) {
ListNode* temp = dummy->next;
dummy->next = dummy->next->next;
delete temp;
return dummy->next;
}
// Move both pointers simultaneously until fast reaches the last node
while (fast != nullptr) {
fast = fast->next;
slow = slow->next;
}
// Remove the nth node
ListNode* temp = slow->next;
slow->next = slow->next->next;
delete temp;
return dummy->next;
}
};- The code uses two pointers,
fastandslow, to find the (n-1)th node from the end. - It then removes the nth node by updating the
nextpointer of the (n-1)th node. - The time complexity of this algorithm is O(L), where L is the length of the linked list, as we traverse the list once.
- The space complexity is O(1) since we are using a constant amount of extra space.
Note: also read about Problems based on Pattern Matching
Follow Me
If you like my post please follow me to read my latest post on programming and technology.
https://www.instagram.com/coderz.py/
https://www.facebook.com/coderz.py
Staying up to the mark is what defines me. Hi all! I’m Rabecca Fatima a keen learner, great enthusiast, ready to take new challenges as stepping stones towards flying colors.
Leave a Comment